601自命题数学

高等数学教学课程大纲

1. 函数与极限

本章节主要教学要求：

1.理解函数概念。

2.了解函数的几种特性：有界性、单调性、奇偶性和周期性。

3.理解复合函数概念，了解反函数的概念。

4.会建立简单实际问题中的函数关系式。

5.理解极限的概念，理解左右极限的定义。会利用定义证明一些简单的极限，了解极限的性质。

6.理解无穷小和无穷大的概念，掌握无穷小的运算性质，会用等价无穷小求极限。

7.掌握极限的运算法则及变量代换法则。

8.理解极限存在的夹逼准则，了解单调有界收敛准则，会用两个重要极限求极限。

9.理解函数在一点连续和在一个区间上连续的概念。

10.了解函数间断点的概念，会判别函数间断点类型。

11.了解初等函数的连续性。了解闭区间上连续函数的性质，并能作一般性的应用。

2. 导数与微分

本章节主要教学要求：

1. 理解导数的概念，了解左右导数的概念。

2. 理解导数的几何意义，会求平面曲线的切线方程和法线方程。

3. 理解函数的可导性与连续性之间的关系。

4. 熟练掌握导数的四则运算法则和复合函数的求导法则，了解反函数的求导法则。

5. 掌握基本初等函数的求导公式。

6. 了解高阶导数的概念，掌握初等函数二阶导数的求法，会求简单函数的 阶导数，会求隐函数和由参数方程所确定的函数的一阶、二阶导数。

7. 理解微分的概念，掌握函数可导与可微的关系，了解微分的几何意义，了解微分的运算法则和一阶微分形式不变性，掌握微分的简单应用。

3. 微分中值定理与导数应用

本章节主要教学要求：

1. 理解费马引理、罗尔定理和拉格朗日定理，了解柯西定理。

2. 掌握用洛必达法则求各类未定式极限的方法。

3.了解泰勒定理，知道e^x、sinx、cosx、ln（1+x）与（1+x）^a等函数的麦克劳林公式。

4. 掌握函数单调性的判断，会利用函数单调性证明某些不等式和方程根的唯一性。

5. 会判断曲线的凸凹性，会求曲线的拐点。

6. 理解函数极值的概念，掌握求极值的方法；掌握函数最大值和最小值的求法，会求解较简单的最大值和最小值的应用问题。

7. 会求曲线的水平与铅直渐近线，会利用导数描绘函数的图形。

8.了解弧微分、曲率和曲率半径的概念，会求弧微分，会计算曲率和曲率半径。

4. 不定积分

本章节主要教学要求：

1. 理解原函数和不定积分的概念，掌握不定积分的性质。

2. 熟练掌握不定积分的基本公式。

3. 掌握不定积分的两类换元法和分部积分法。

4. 会求简单有理函数、简单三角函数有理式和简单无理函数的不定积分。

5. 定积分及其应用

本章节主要教学要求：

1. 理解定积分的概念，掌握定积分的性质，了解函数可积的充分条件。

2. 熟悉积分上限函数及其求导方法。

3. 熟练掌握牛顿-莱布尼兹公式。

4. 掌握定积分的换元法和分部积分法。

5. 理解两类反常积分的概念，会计算一些简单的反常积分。

6. 掌握定积分的元素法。

7. 掌握平面图形面积、立体体积、平面曲线弧长等几何量的计算。

8. 会求变力做功、液体的侧压力和引力等简单的物理量。

6. 微分方程

本章节主要教学要求：

1．了解微分方程、微分方程的阶、微分方程的解、通解、初始条件、特解等概念。

2．掌握可分离变量方程和一阶线性方程的解法，会解齐次方程，了解伯努利方程的解法，了解会用变量代换求解方程的方法。

3．会用降阶法求解形如

的微分方程。

4．掌握二阶线性微分方程解的结构。

5．掌握二阶常系数齐次线性微分方程的解法，了解高阶常系数齐次线性微分方程的解法。

6．会求 的二阶常系数非齐次线性微分方程，

了解 的二阶常系数非齐次线性微分方程的解法。

7．会用微分方程解一些简单的几何和物理问题。

7. 多元函数微分法及其应用

本章节主要教学要求：

1．理解多元函数的概念，了解点函数的概念，会求多元函数的函数值，会求二元函数的定义域，了解二元函数的几何图形。

2．了解二元函数的极限与连续的概念，了解有界闭区域上连续函数的性质。

3．理解多元函数偏导数的概念，掌握偏导数和二阶偏导数的求法，了解二阶以上偏导数的求法，知道偏导数存在与函数连续的关系，了解偏导数的几何意义。

4．理解全微分的概念，知道可微的必要与充分条件，会求多元函数的全微分。

5．掌握多元复合函数一阶偏导数的求法，了解多元复合函数二阶偏导数的求法。

6．了解隐函数存在定理，掌握由一个方程所确定的隐函数的一阶导数或偏导数求法，了解其二阶导数或偏导数求法，了解由两个方程所确定的隐函数的一阶导数或偏导数求法。

7．了解曲线的切线与法平面方程的求法，了解曲面的切平面与法线方程的求法。

8．理解方向导数和梯度的概念，会求方向导数和梯度，知道方向导数与梯度的关系。

9．理解多元函数极值和条件极值的概念，掌握多元函数极值的必要条件和二元函数极值的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求一些较简单的最大值和最小值的应用问题。

8. 重积分

1．本章节主要教学要求：

2．理解二重积分的概念，了解二重积分的性质。

3．掌握利用直角坐标、极坐标计算二重积分的方法，会在直角坐标系下交换二次积分次序，会将直角坐标、极坐标下的二次积分互化。

4．会用重积分表示一些简单的几何量（如平面面积、立体体积、曲面面积等）和简单的物理量（如质量、质心、转动惯量、引力等）。

9. 无穷级数

本章节主要教学要求：

1．理解无穷级数收敛、发散以及和的概念，知道无穷级数的基本性质，掌握无穷级数收敛的必要条件。

2．掌握几何级数和 -级数的收敛性。

3．掌握正项级数的比较审敛法、比较审敛法的极限形式、比值审敛法，了解正项级数的根值审敛法，知道正项级数收敛的充分必要条件。

4．掌握交错级数的莱布尼兹审敛法，会估计交错级数的截断误差。

5．知道无穷级数绝对收敛与条件收敛的概念，了解绝对收敛级数的性质。

6．了解函数项级数的收敛域及和函数的概念。

7．掌握阿贝尔定理，掌握幂级数的收敛半径和收敛区间的求法，了解收敛域的求法。

8．了解幂级数在其收敛域内的基本性质，会求简单幂级数的和函数。

9．了解函数展开为泰勒级数的充分必要条件，了解将函数展开为幂级数的直接展开法，会利用函数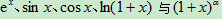 的麦克劳林展开式将一些简单的函数间接展开成幂级数。

 

线性代数教学大纲

第一章  行列式

本章主要教学要求：掌握行列式的六个主要性质，会运用这些性质进行行列式的简化。理解代数余子式的概念，掌握行列式按行(列)展开从而降阶的方法。对于确定阶数(≤4阶)的行列式，会通过化简为三角形行列式求值，或化简后展开、降阶计算；对于简单的不定阶数的行列式(n阶)，会根据其特点计算其值。了解拉普拉斯定理，理解克拉默法则，掌握其关于齐次方程组的推论。

第二章 矩阵

本章主要教学要求：理解矩阵的概念(包括矩阵的元素、阶数)，掌握矩阵的表示法。了解一些常用的特殊矩阵，如行(列)矩阵、零矩阵、方阵、上(下)三角阵、单位阵等。掌握矩阵的加法、数乘、乘法、转置运算及其运算律，理解矩阵一般不可交换和不可消去的原理。理解线性变换和线性方程组的矩阵形式，掌握方阵的幂运算，理解对称阵的定义及其性质。掌握方阵可逆的定义及其充要条件，掌握用伴随阵求逆矩阵的方法，掌握用逆矩阵解线性方程组和简单矩阵方程的方法。理解矩阵的行(列)初等变换及矩阵的等价性概念，掌握矩阵的行初等变换。理解矩阵秩的定义，掌握用初等变换求矩阵秩的方法。理解初等矩阵的定义及其性质，掌握用初等变换求逆矩阵的方法，了解分块矩阵的概念。

第三章      向量与线性方程组

本章主要教学要求：掌握用方程组的增广矩阵(或系数矩阵，对于齐次方程组)作行初等变换解方程组的一般方法。理解n维向量的概念，掌握向量的线性运算。理解线性组合、线性表示等概念，理解向量组线性相关、线性无关的定义和充要条件，掌握判别向量组线性相关性的基本方法，会用定义和充要条件进行简单的论证。理解向量组最大无关组的定义和性质，理解向量组秩的定义，会求向量组的最大无关组。了解齐次方程组解空间的概念，掌握基础解系和通解的求法；会求非齐次方程组的通解。理解向量的内积、夹角等概念，理解向量正交的概念，掌握向量组的正交化方法，了解正交阵的定义及其性质。

第四章  矩阵的特征值与特征向量

本章主要教学要求：理解方阵特征值和特征向量的定义及其主要性质，掌握特征值和特征向量的求法。理解方阵相似变换的定义，理解方阵对角化的定义和方阵可对角化的充要条件，掌握用正交变换将实对称矩阵对角化的方法。

 

 

推荐书目：

高等数学（上、下） 同济第六版  高教出版社

线性代数 吴天毅 王玉杰 邱玉文编 高等教育出版社 2011.1